Demo example#

The corresponding jupyter notebook script can be downloaded here.

The necessary input data (surfaces + muscles description) can be downloaded here:.

Import libraries#

We start by importing necessary libraries. Myoelectric digital twin is part of the neurodec software. Apart from standard auxilitary libraries we also need meshio library to work with .stl surfaces

%config Completer.use_jedi = False

import glob
import os
import json

import matplotlib.pyplot as plt
import trimesh
import numpy as np

import neurodec as nd

nd.mdt._API_URL = "http://35.173.188.106:8001/"
nd.mdt.wait = False  # Set to true to wait step by step.

Load model surfaces#

Subject’s forearm anatomy is represented by .stl meshes of the different tissue surfaces: upper skin, lower skin, individual muscles and bones.

The surface filename for each muscle is stored in muscles_description.json file.

We load each mesh with meshio package and create a nd.mdt.Surface for each tissue surface.

def load_surface(filename: str):
    mesh = trimesh.load_mesh(filename)
    return mesh.vertices, mesh.faces

MODEL_DIR = "/<your-data-path>/right-arm-template"

muscles_description_fname = os.path.join(MODEL_DIR, 'muscles_description.json')
with open(muscles_description_fname) as f:
    muscles_description = json.load(f)

bones = []
for filename in glob.glob(os.path.join(MODEL_DIR, 'bones', '*.stl')):
    vertices, triangles = load_surface(filename)
    bones.append(nd.mdt.Surface.new(vertices, triangles, nd.mdt.SurfaceType.BONE))

muscles = []
for muscle in muscles_description['muscles']:
    fname = os.path.join(MODEL_DIR, 'muscles', muscle['fname'])
    vertices, triangles = load_surface(fname)
    muscles.append(nd.mdt.Surface.new(vertices, triangles, nd.mdt.SurfaceType.MUSCLE, label=muscle['label']))

skins = []

filename = os.path.join(MODEL_DIR, 'skin', 'inner.stl')
vertices, triangles = load_surface(filename)
skins.append(nd.mdt.Surface.new(vertices, triangles, nd.mdt.SurfaceType.INNER_SKIN))

filename = os.path.join(MODEL_DIR, 'skin', 'outer.stl')
vertices, triangles = load_surface(filename)
skins.append(nd.mdt.Surface.new(vertices, triangles, nd.mdt.SurfaceType.OUTER_SKIN))

print([str(s) for s in skins])

['Surface(26, Status.READY, SurfaceType.INNER_SKIN)', 'Surface(27, Status.READY, SurfaceType.OUTER_SKIN)']

Generate volume conductor#

Volume conductor is a function of anatomy surfaces and conductivities per tissue. Here, the default conductivity values are used.

conductor = nd.mdt.Conductor.new(bones + muscles + skins)

Generate bracelet elctrodes#

We generate a bracelet of electrodes made of ten rings. Each ring has 16 equidistant electrodes of 3mm radius. Disctance between rings is 9 mm.

Note that user can create electrodes by directly providing their centers and radii with nd.mdt.Electrode.new(location, radius).

outer_skin_surface = skins[1]
radius = 0.003  # in meters
first_electrode_location = np.array([-0.247705, -0.083379, 0.838751])
rings_normal = np.array([0.17797643704463834, 0.19429176558661732, 0.9646632042750106])
n_rings = 10
distance_between_rings = 0.009  # in meters
n_electrodes_per_ring = 16

bracelet = nd.mdt.ElectrodeBracelet.new(
    outer_skin_surface, radius, first_electrode_location, rings_normal,
    n_rings, distance_between_rings, n_electrodes_per_ring)

You can save generated electrodes as spheres with trimesh for futher visualization

print(bracelet.electrodes[0].location)

for i, electrode in enumerate(bracelet.electrodes):
    sphere = trimesh.creation.icosphere()
    sphere.vertices = sphere.vertices * electrode.radius
    sphere.vertices = sphere.vertices + electrode.location
    sphere.export(MODEL_DIR + f'/elec_{i}.stl')

Generate forward solver#

Forward solver is a function of volume conductor and electrodes

forward_solution = nd.mdt.ForwardSolution.new(conductor, bracelet.electrodes)

Generate fiber geometry#

User can directly provide the number of fibers, or it can be automatically estimated from the avarage fiber radius.

Start and ending planes for fibers are stored in the muscle_description.

fibers_per_muscle = []
for i, muscle in enumerate(muscles):
    plane_origins = muscles_description['muscles'][i]['plane_origins']
    plane_normals = muscles_description['muscles'][i]['plane_normals']
    fibers = nd.mdt.Fibers.new(muscle, plane_origins, plane_normals)
    fibers_per_muscle.append(fibers)

Generate fiber basis#

Fiber basis is a function of fibers and forward solution.

fiber_basis_per_muscle = []
for i, fibers in enumerate(fibers_per_muscle):
    fiber_basis = nd.mdt.FiberBasis.new(fibers, forward_solution)
    fiber_basis_per_muscle.append(fiber_basis)

Compute MUAPs#

To compute MUAPs for each muscle, fiber properties and motor units (MUs) should be generated and a sampling frequancy (in Hz) should be provided.

Here, fiber properties are generated using default tendon, velocity and neuromascular junction values.

The number of MU should be specified. Here, default values for minimum and maximum relative MU areas are used.

SAMPLING_FREQUENCY = 8000
n_motor_units = 150

muaps_per_muscle = []
for fibers, fiber_basis in zip(fibers_per_muscle, fiber_basis_per_muscle):

    fiber_properties = nd.mdt.FiberProperties.new(fibers)

    motor_units = nd.mdt.MotorUnits.new(fibers, n_motor_units)

    muaps = nd.mdt.MotorUnitsActionPotentials.new(fibers, fiber_basis, fiber_properties, motor_units,
                                                  SAMPLING_FREQUENCY)
    muaps_per_muscle.append(muaps)

Simulate a simple movement#

def single_muscle_activation(max_mvc, duration, peak_time, fs):
    n_time_samples = int((peak_time + duration / 2.) * fs)
    t = np.linspace(-np.pi / 2, np.pi + np.pi / 2, int(duration * fs))
    waveform = max_mvc * 0.5 * (np.sin(t) + 1.)
    i_0 = n_time_samples - len(waveform)
    muscle_activation = np.zeros(n_time_samples)
    muscle_activation[i_0:] = waveform
    return muscle_activation

def generate_movement(n_muscles, mean_max_mvc, std_max_mvc, duration, peak_time, fs):
    muscle_activations = []
    for i in range(n_muscles):
        max_mvc = np.random.uniform(mean_max_mvc - std_max_mvc,
                                    mean_max_mvc + std_max_mvc)
        max_mvc = np.clip(max_mvc, 0., 100.)
        muscle_activations.append(single_muscle_activation(max_mvc, duration, peak_time, fs))
    return muscle_activations

Print the list of muscle labels

for i, muscle in enumerate(muscles):
    print(i, muscle.label)

Extensor carpi radialis longus
Extensor carpi radialis brevis
Extensor carpi ulnaris
Flexor carpi radialis
Palmaris longus
Flexor carpi ulnaris humeral head
Flexor carpi ulnaris ulnar head
Pronator teres humeral head
Pronator teres ulnar head
Pronator quadratus
Supinator
Brachioradialis
Flexor digitorum superficialis humeroulnar head
Flexor digitorum superficialis radial head
Abductor pollicis longus
Anconeus
Extensor digiti minimi
Extensor digitorum
Extensor indicis
Extensor pollicis brevis
Extensor pollicis longus
Flexor digitorum profondus
Flexor pollicis longus

Select wrist extensors

muscle_idx = [0, 1, 2]

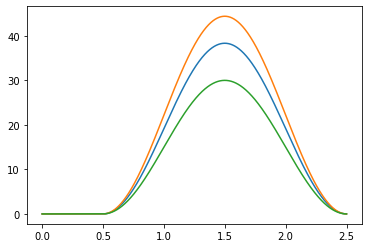
Generate a simple 2 second long muscle activation patern corresponding to a wrist extension of around 40%MVC at its peak.

np.random.seed(1)
n_muscles = len(muscle_idx)
mean_max_mvc = 40 # %MVC
std_max_mvc = 10 # add some inter muscle variability in %MVC
duration = 2. # sec
peak_time = 1.5 # sec
activations = generate_movement(n_muscles, mean_max_mvc, std_max_mvc, duration, peak_time, SAMPLING_FREQUENCY)

for single_activation in activations:
    times = np.arange(len(single_activation)) / SAMPLING_FREQUENCY
    plt.plot(times, single_activation)

Generate impulse trains for each muscle of interest

impulse_trains_per_muscle = []
for muscle_id, single_activation in zip(muscle_idx, activations):
    impulse_trains_per_muscle.append(nd.mdt.ImpulseTrains.new(muaps_per_muscle[muscle_id],
                                                              single_activation,
                                                              random_seed=0))

Assemble raw sEMG signal from muaps and impulse trains, and load the resulting data.

emg_per_muscle = []
for impulse_trains in impulse_trains_per_muscle:
    emg = nd.mdt.Electromyography.new(impulse_trains)
    emg.wait() # wait for the computation to finish before loading the EMG data
    emg_per_muscle.append(emg.data.copy())

Sum up EMG signals of individual muscles

min_length = np.min([e.shape[1] for e in emg_per_muscle])
emg_total = np.sum([e[:, :min_length] for e in emg_per_muscle], axis=0)

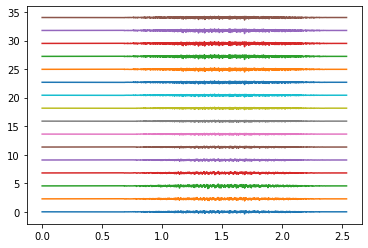
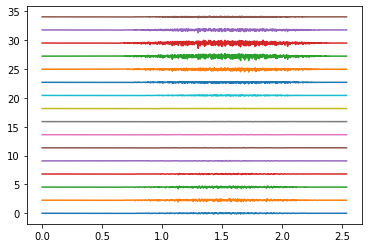
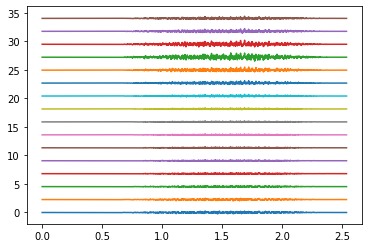
Plot the results

times = np.arange(emg_total.shape[1]) / SAMPLING_FREQUENCY
plot_shift = np.ptp(emg_total)
rings_to_plot = [0, 4, 9]

for ring in rings_to_plot:
    emg_to_plot = emg_total[ring*16:(ring+1)*16]
    plt.figure()
    plt.plot(times, emg_to_plot.T + plot_shift * np.arange(16))
    plt.show()